FreeFem++ Source Code Review

This post is an ongoing effort to document my findings as I walk through the source code of a tool I really like, FreeFem++.

Given a concise description of a PDE weak formulation / variational form as well as a set of boudary conditions, ff++ will automagically discretize and solve the PDE. Thanks to its domain specific language it’s also possible to build more advance numerical methods on top of the FE solver itself (domain decomposition, multi-physics, …).

This is a good tool if you’re tired of writting ad-hoc solvers from scratch each time you need to perform a FE analysis. Of course before using such a tool it’s nice to clearly understand what’s going on under the hood.

Similar tools are

• FEnics;
• the MATLAB PDE toolbox

Codebase srtucture

Here is the structure of the src directory containing most of ff++ source code (excluding dependencies):

ff++$ tree -d src
src
├── agl
├── Algo
├── bamg
├── bamglib
├── bin-win32
├── Eigen
├── femlib
├── fflib
├── glx
├── Graphics
├── iml
├── lglib
├── libMesh
├── medit
├── mpi
├── nw
├── solver
├── std
└── x11

The directories I’m particularly interested in are:

• fflib: lexer, abstract syntax tree data structures & interpreter, high level assembly and resolution of discretized PDE;
• lglib: the grammar definition for the ff++ language;
• femlib: low level assembly of discretized PDE, various FE families implementation (P1, P2, Raviart-Thomas …) as well as matrix and vector definitions;
• solver: mainly wrappers to sparse direct solvers such as UMFPACK, MUMPS, pardiso as well as sparse iterative solvers such as HYPRE, HYPS, pARM etc.

Stuff I’m not too intersted in:

• The bamg and bamglib directories contain all the 2D mesh generation code: bamg stands for Bidimensional Anisotropic Mesh Generator and is the name of a stand alone 2D mesh generation tool written by Frédéric Hecht, the main author of ff++. It comes with a library you can re-use in your own project. The 3D mesh generation relies on Tetgen;
• The Algo, Eigen and iml directories contain implementation of iterative methods for solving linear systems (CG, GMRES, …) and find eigen values/vectors;
• The libMesh directory contains the code of the libMesh library defining mesh datastructures and the corresponding read/write functions.

Language

ff++ language is imperative. It borrows some syntax from C++. For example the stream operators (<< and >>) to perform formated I/Os which is not really the best part of C++ …

Lexer

The hand written lexer (class mylex) lives in fflib/lex.hpp.

Parser

The parser is using GNU Bison. Its grammar is described in the lglib/lg.ypp file. I guess the lg prefix stands for “language”. That prefix is used in other places in the code base. For example: fflib/lgfem.hpp, fflib/lgmesh.hpp, fflib/lgmat.cpp, etc where the language builtin types and functions are defined. This convention doesn’t seem to be enforced though.

The generated parser entry point is called yyparse() (it’s #defined to lgparse)

The first frames of a typical call stack look like this:

#0  yyparse () at lg.tab.cpp:1851
#1  Compile () at lg.ypp:777
#2  mainff (argc=2, argv=0x7fffffffddf8) at lg.ypp:947
#3  main (argc=2, argv=0x7fffffffddf8) at ../Graphics/sansrgraph.cpp:199

Now, even though yyparse() is called by a function called Compile() and ff++ outputs messages such as

times: compile 0.100339s, execution 89.3461s

the language is not compiled: no machine or byte code is generated whatsoever. It’s more of an interpreter.

Interpreter

In ff++, the Bison semantic actions do not usually interprete statements on the fly. Instead an abstract syntax / expression tree is built using types defined in fflib/AFunction.hpp, fflib/AFunction2.hpp, fflib/Operator.hpp, etc.

An exception would be the load statement which will trigger a call to bool load(string ss) defined in fflib/load.cpp, loading shared objects (aka “plugins”) on the fly.

In the top level semantic action, executed once the end of file is reached, the tree is walked and statements are interpreted:

start:   input ENDOFFILE {
	[...]
	size_t sizestack = currentblock->size()+1024;
	[...]
	Stack stack = newStack(sizestack);
	[...]
	$1.eval(stack);
	[...]
}

In this Bison/C++ code snipet S1 is the result of the input semantic action and is of type class CListOfInst defined in fflib/AFunction.hpp.

Ultimately the call to CListOfInst::eval will execute this method which can be seen as the interpreter’s main loop: :

AnyType ListOfInst::operator()(Stack s) const {     
    AnyType r; 
    double s0=CPUtime(),s1=s0,ss0=s0;
    StackOfPtr2Free * sptr = WhereStackOfPtr2Free(s);
    try { // modif FH oct 2006 
	for (int i=0;i<n;i++) 
	{
	    TheCurrentLine=linenumber[i];
	    r=(*list[i])(s);
	    sptr->clean(); // modif FH mars 2006  clean Ptr
	    s1=CPUtime();
	    if (showCPU)  
		cout << " CPU: "<< i << " " << s1-s0 << "s" << " " << s1-ss0 << "s" << endl;
	    s0=CPUtime();
	}
    }
    catch( E_exception & e) 	
    {
	if (e.type() != E_exception::e_return)  
	    sptr->clean(); // pour ne pas detruire la valeur retourne  ...  FH  jan 2007
	throw; // rethow  
    }
    catch(...)
    {
	sptr->clean();
	throw; 
    }
    return r;
}

By the way, often the code is mixing (broken) English and French which is not making it easier to dive into the codebase.

Once parsing is complete and the interpreter starts doing its job, the call stack should look like this:

#0  ListOfInst::operator() at AFunction2.cpp:793
#1  eval at ./../fflib/AFunction.hpp:1459
#2  yyparse () at lg.tab.cpp:1851
#3  Compile () at lg.ypp:777
#4  mainff (argc=2, argv=0x7fffffffddf8) at lg.ypp:947
#5  main (argc=2, argv=0x7fffffffddf8) at ../Graphics/sansrgraph.cpp:199

Activation record

Storage for variables within the current lexical scope is allocated on a stack of type struct StackType defined in fflib/ffstack.hpp (typedef-ed to StackType & Stack;). The stack is allocated just before walking the expression tree (see the ENDOFFILE semantic action).

Offsets of local variables within the stack and the stack size itself (“currentblock->size()”) are computed in the semantic actions. Every time a new variable declaration is encountered, an object of class LocalVariable is created to keep track of its type and offset. The Block and TableOfIdentifier classes defined in fflib/AFunction.hpp handle the traditional symbol table as well as the top of the stack offsets/pointers. Here is roughly the executuin flow:

• Semantic action for a simple declaration asking the current block to allocate a new local variable:

declaration: type_of_dcl {dcltype=$1} list_of_dcls ';' {$$=$3}
[...]
type_of_dcl: TYPE 
[...]
list_of_dcls: ID {$$=currentblock->NewVar<LocalVariable>($1,dcltype)}  
[...]

• The Block class delegates allocation to a TableOfIdentifier

class Block {

   size_t  top,topmax;
   TableOfIdentifier table;
   ListOfTOfId::iterator itabl; 

   [...]

   	template<class T>   
   	C_F0 NewVar(Key k,aType t) {
		C_F0 r = table.NewVar<T>(k, t,top);
		topmax = Max(topmax,top);
		return r;
   	}

   [...]
}

• The TableOfIdentifier lookup/insert a new LocalVariable and wraps it with an expression tree node of type class C_F0:

template<class T>   
inline  C_F0 TableOfIdentifier::NewVar(Key k,aType t,size_t & top) 
{  
	return t->Initialization(New(k,NewVariable<T>(t,top))); 
}

const  Type_Expr &   TableOfIdentifier::New(Key k,const Type_Expr & v,bool del)
{
	if( this != &Global) {
		if ( Global.m.find(k) != Global.m.end() )
		{
			if(mpirank==0 && (verbosity>0))
			  cerr << "\n *** Warning  The identifier " << k << " hide a Global identifier  \n";
		}
	}

	pair<iterator,bool>  p=m.insert(pKV(k,Value(v,listofvar,del)));
	listofvar = &*m.find(k);
	if (!p.second) 
	{
	    if(mpirank==0) {
		cerr << " The identifier " << k << " exists \n";
		cerr << " \t  the existing type is " << *p.first->second.first << endl;
		cerr << " \t  the new  type is " << *v.first << endl;
	    }
	    CompileError();
	}

	return v;
}

template<class T>
inline Type_Expr  NewVariable(aType t,size_t &off) 
{ 
	size_t o= align8(off);//  align    
	//  off += t->un_ptr_type->size;
	// bug    off += t->size;
	off += t->un_ptr_type->size; // correction 16/09/2003 merci à Richard MICHEL
	return  Type_Expr(t,new T(o,t));
}

A simple “int a;” statement call stack looks like this:

#0  NewVariable<LocalVariable> (off=@0x1063218: 48, t=0xfe5ad0) at ./../fflib/AFunction.hpp:1839
#1  TableOfIdentifier::NewVar<LocalVariable> (this=this@entry=0x1063228, k=0x1058ba0 "a", t=0xfe5ad0, top=@0x1063218: 48) at ./../fflib/AFunction.hpp:1890
#2  NewVar<LocalVariable> (t=<optimized out>, k=<optimized out>, this=0x1063210) at ./../fflib/AFunction.hpp:2096
#3  lgparse () at lg.ypp:386
#4  Compile () at lg.ypp:777
#5  mainff (argc=2, argv=0x7fffffffde08) at lg.ypp:947
#6  main (argc=2, argv=0x7fffffffde08) at ../Graphics/sansrgraph.cpp:199

Builtins

Work in progress !

Matrices, FESpace, Varform, Problem …

PDE discretization

The best way to figure out how PDE discretization is achieved is to run the script hereunder and step through with the debugger:

mesh Th = square(5,5);
fespace Vh(Th,P1);
varf a(u,v) = int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v))
+ on(1,2,3,4,u=0) ;
matrix A=a(Vh,Vh);

The interesting statement is “matrix A=a(Vh,Vh);”. It triggers:

• allocation of a CSR encoded sparse matrix;
• numerical integration and assembly of the elementary matrices

Assembly

The expression tree node corresponding to that statement is of type class OpMatrixtoBilinearForm<R,v_fes>::Op. It is defined in fflib/problem.hpp. The interpreter will call the AnyType OpMatrixtoBilinearForm<R,v_fes>::Op::operator()(Stack stack) const method defined in the same file. We can summarize that method like so:

AnyType OpMatrixtoBilinearForm<R,v_fes>::Op::operator()(Stack stack) 
{
	[...]
	A.A.master( new  MatriceMorse<R>(Vh,Uh,VF) );
	*A.A=R(); // reset value of the matrix
	if ( AssembleVarForm<R,MatriceCreuse<R>,FESpace >( stack,Th,Uh,Vh,ds.typemat->sym,A.A,0,b->largs) )
		AssembleBC<R,FESpace>( stack,Th,Uh,Vh,ds.typemat->sym,A.A,0,0,b->largs,ds.tgv);
	[...]
}

• First the call to the MatriceMorse constructor will in turn call void MatriceMorse<R>::Build(const FESpace & Uh, const FESpace & Vh, bool sym, bool VF) defined in femlib/MatriceCreuse_tpl.hpp. This is responsible for computing the profile of the CSR encoded sparse matrix (French people say “Morse” encoding).

Here is a version of that method I commented

• Then the calls to AssembleVarForm will compute the elementary matrices and assemble them into the stiffness matrix. AssembleVarForm will walk all the elementary integrals of the variational form and delegate the computation to a more specialized method. For example if an elementary integral defines a bilinear form, void AssembleBilinearForm(Stack stack,const Mesh & Th,const FESpace & Uh,const FESpace & Vh,bool sym, MatriceCreuse<R> & A, const FormBilinear * b) will be called.

Work in progress !

DoF numbering

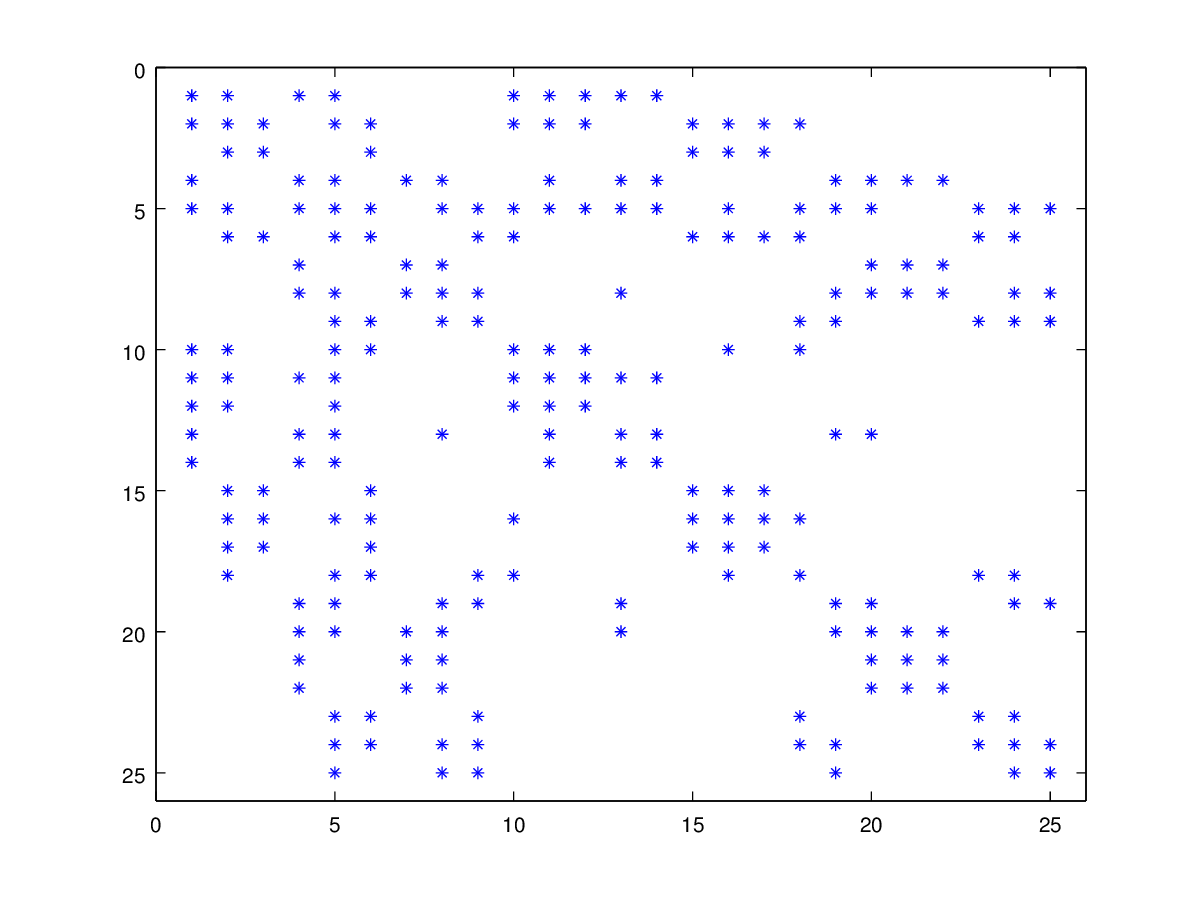
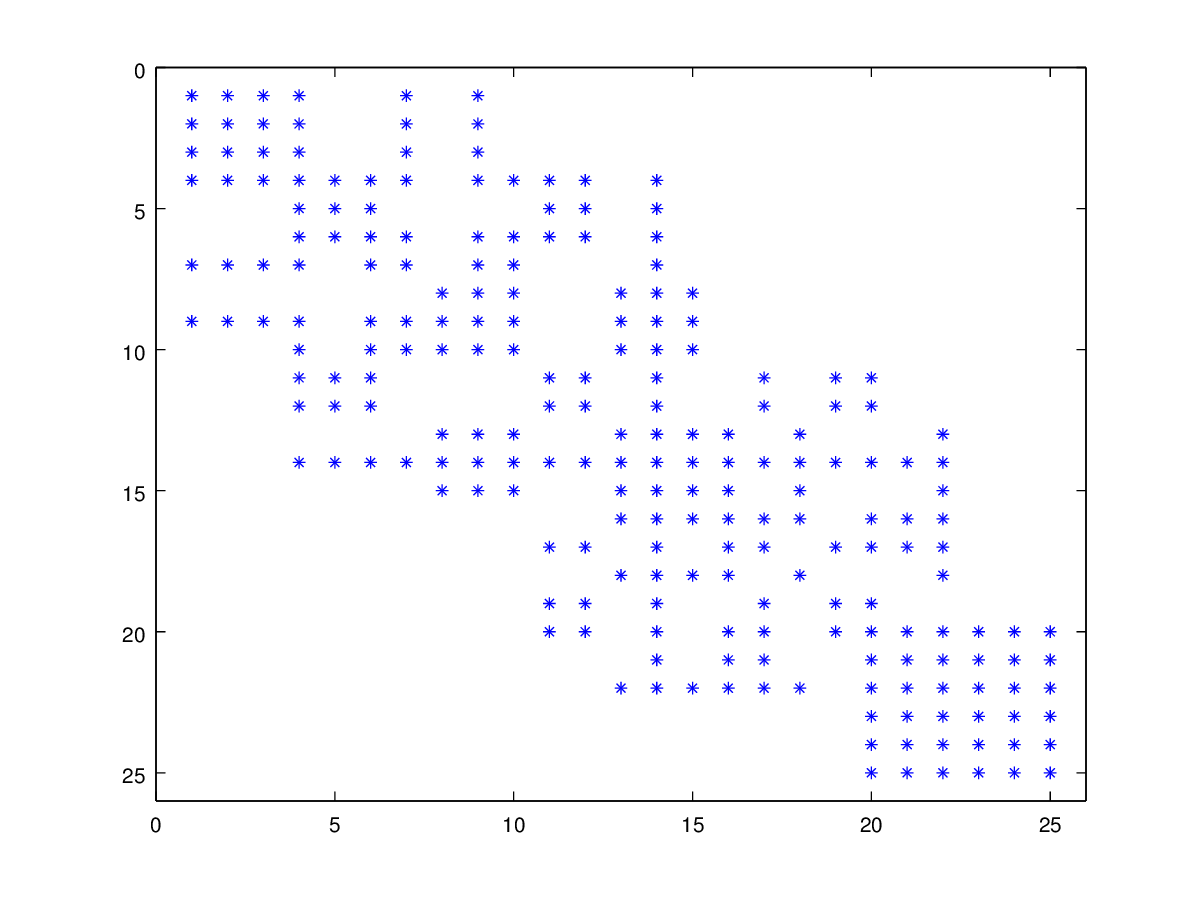
Numbering is a 3 stages process:

• dummy numbering of the vertices, edges, faces, volumes, in ff++ these are called “nodes”;
• reduce the skyline profile of that initial node numbering using the Gibbs-Poole-Stockmeyer algorithm;
• build a DoF numbering from the improved node numbering: this is simply done by running a prefix sum of the number of DoF per node following the computed node numbering.

Here is a commented simplified (no periodic boundary conditions, no mortar method) version of stage 1. The original version can be found in femlib/FESpace.cpp.

The original paper describing the Gibbs-Poole-Stockmeyer used by stage 2 can be found here. The ff++ implementation is found in femlib/gibbs.cpp.

Spy (2x2 square, 9 vertices, 8 triangles) after stage 1:

Spy after stage 2 (GPS algorithm)

Numerical integration

Work in progress !